Frecuency factor Kt estimation for the incomplete gamma probability distribution

Article Sidebar

Figura 1. Valores del factor de frecuencia ‘KT’ para diferentes probabilidades de excedencia de la precipitación total mensual para la FDP Gamma Incompleta
Published: Apr 9, 2025
Keywords:
frequency factor, reduced variable model, exceedance probability

Main Article Content

Lorenzo Armando Aceves Navarro
Colegio de Postgraduados
https://orcid.org/0000-0002-9301-9223
Benigno Rivera Hernández
Universidad Popular de la Chontalpa
https://orcid.org/0000-0003-1713-4710
José Francisco Juárez López
Colegio de Postgraduados
https://orcid.org/0000-0002-7145-1509
Agrícola Arrieta Rivera
Tecnológico Nacional de México
https://orcid.org/0000-0003-4169-112X

Abstract

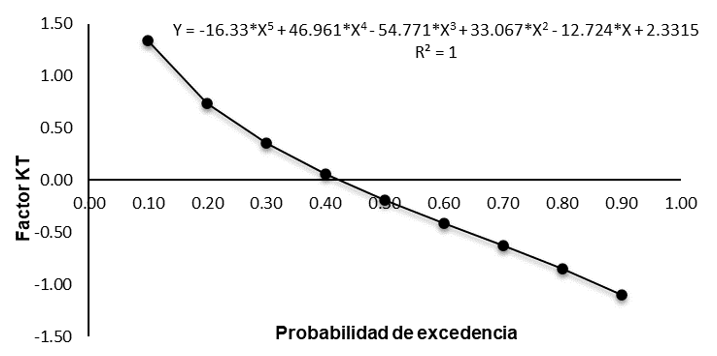
In the present paper, a procedure is presented to obtain the value of the frequency factor for the Incomplete Gamma Probability Distribution Function from their ​​shape (α) and scale (β) parameters. Using regression analysis, the rainfall data resulting from applying the model of the reduced variable were compared with those obtained with the Incomplete Gamma Function. Data from 53 years of total monthly rainfall from the meteorological station 27039 Samaria, Cunduacán, Tabasco were used to adjust and calibrate the values ​​of the frequency factor KT. Likewise, the values ​​of total monthly rainfall from five meteorological stations from various rainfed regions of Mexico were selected, with records ranging from 31 to 59 years. Data from the meteorological stations of Motul de Felipe Carrillo Puerto, Yucatán; Texcoco, State of Mexico; Suchiate, Chiapas; Zapopan, Jalisco; and Acaponeta, Nayarit to validate the resulting values ​​of the KT frequency factor. The Pearson correlation coefficient in the adjustment, calibration, and validation processes was higher than 0.997. Thus, the resulting KT values ​​had a very good fit and are reliable for calculating the probability of exceeding the total monthly rainfall for an Incomplete Gamma Function.

Downloads

Download data is not yet available.

Article Details

How to Cite
Aceves NavarroL. A., Rivera HernándezB., Juárez LópezJ. F., & Arrieta RiveraA. (2025). Frecuency factor Kt estimation for the incomplete gamma probability distribution. Revista Cubana De Meteorología, 31(2), https://cu-id.com/2377/v31n2e06. Retrieved from http://rcm.insmet.cu/index.php/rcm/article/view/955
Issue
Vol 31 No 2 (2025): abril-junio
Section
Original Articles
Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Those authors who have publications with this journal accept the following terms of the License Attribution-NonCommercial 4.0 International (CC BY-NC 4.0):

You are free to:

  • Share — copy and redistribute the material in any medium or format
  • Adapt — remix, transform, and build upon the material

The licensor cannot revoke these freedoms as long as you follow the license terms.

Under the following terms:

  • Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
  • NonCommercial — You may not use the material for commercial purposes.
  • No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.

The journal is not responsible for the opinions and concepts expressed in the works, they are the sole responsibility of the authors. The Editor, with the assistance of the Editorial Committee, reserves the right to suggest or request advisable or necessary modifications. They are accepted to publish original scientific papers, research results of interest that have not been published or sent to another journal for the same purpose.

The mention of trademarks of equipment, instruments or specific materials is for identification purposes, and there is no promotional commitment in relation to them, neither by the authors nor by the publisher.

References

Arroyo, I.; Bravo, L. C.; Llinás, H. & Muñoz, F. L. 2014. “Poisson and gamma distributions: A discrete and continuous relation”. Prospectiva, 12(1): 99-107. https://doi.org/10.15665/rp.v12i1.156.
Bokke, A. S. & Shoro, K. E. 2020. “Impact of effective rainfall on net irrigation water requirement: The case of Ethiopia”. Water Science, 34(1): 155-163. https://doi.org/10.1080/11104929.2020.1749780.
Chow, V. T. 1951. “A general formula for hydrologic frequency analysis”. Eos, Transactions American Geophysical Union, 32(2): 231-237. https://doi.org/10.1029/TR032i002p00231.
Evin, G.; Merleau, J. & Perreault, L. 2011. “Two‐component mixtures of normal, gamma, and gumbel distributions for hydrological applications”. Water Resources Research, 47(8): W08525. https://doi.org/10.1029/2010WR010266.
Hargreaves, G. H. & Jensen, D. T. 2002. Simplification of planning to meet future demands for food and water. Energy: Climate, Environment and Water-Issues and Opportunities for Irrigation and Drainage, 513. Disponible: https://hdl.handle.net/10217/206923. [Consultado: Enero 11, 2024].
Husak, G. J.; Michaelsen, J. & Funk, C. 2007. “Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring applications”. International Journal of Climatology, 27(7): 935-944. https://doi.org/10.1002/joc.1441.
IMTA (Instituto Mexicano de Tecnología del Agua). 2009. ERIC III: Extractor Rápido de Información Climatológica v.2. CD, p. 28.
Jadhav, M. G.; Aher, H. V.; Jadhav, A. S. & Gote, G. N. 2015. “Crop Planning Based on Moisture Adequacy Index (MAI) of Different Talukas of Aurangabad District of Maharashtra”. Indian J. Dryland Agric. Res. & Dev, 30(1): 101-103. https://doi.org/10.5958/2231-6701.2015.00016.0.
Johnson, R. A., Miller, I., & Freund, J. E. 2018. Ninth Ed. Probability and statistics for engineers. Pearson Education Ltd.
Kite, G. W. 1977. Frequency and risk analyses in hydrology (Chapter 9, pp. 105-122 and chapter 12, 156-168). Fort Collins, USA: Water Resources Publications. https://es.scribd.com/document/487410158/Frequency-and-Risk-Analyses-in-Hidrology-G-W-Kite.
Laux, P.; Wagner, S.; Wagner, A.; Jacobeit, J.; Bárdossy, A. & Kunstmann, H. 2009. “Modelling daily precipitation features in the Volta Basin of West Africa”. International Journal of Climatology: A Journal of the Royal Meteorological Society, 29(7): 937-954. https://doi.org/10.1002/joc.1852.
Machado-Fernández, J. R. 2016. Modelación de la Distribución Gamma en MATLAB para Aplicaciones de Radar. Ciencias Holguín, 22(4), 1-17. https://www.redalyc.org/pdf/1815/181548029005.pdf.
Nkegbe, P. K. & Shankar, B. 2014. “Adoption intensity of soil and water conservation practices by smallholders: evidence from Northern Ghana”. Bio-based and Applied Economics, 3(2): 159-174. https://doi.org/10.13128/BAE-13246.
Sahu, T.; Chaudhary, J. L. & Sahu, K. K. 2022. “Analysis of Rainfall Probabilities and Crop Planning for Different Districts of Chhattisgarh”. International Journal of Environment and Climate Change, 12(10): 858-862. https://doi.org/10.9734/ijecc/2022/v12i1030873.
Sharma, M. A. & Singh, J. B. 2010. “Use of probability distribution in rainfall analysis”. New York Science Journal, 3(9): 40-49. https://www.sciencepub.net/newyork/ny0309/07_3294ny0309_40_49_02.pdf.
Stöckle, C. O., J. Kjelgaard, and G. Bellocchi (2004), Evaluation of estimated weather data for calculating Penman-Monteith reference crop evapotranspiration, Irrig. Sci., 1, 39–46. https://doi.org/10.1007/s00271-004-0091-0
Vergni, L.; Todisco, F.; Di Lena, B., & Mannocchi, F. 2020. “Bivariate analysis of drought duration and severity for irrigation planning”. Agricultural Water Management, 229, 105926. https://doi.org/10.1016/j.agwat.2019.105926.
Wilks, D. S. 2006. Statistical methods in the atmospheric sciences. Second Edition. International Geophysics Series, Vol. 91. Academic press. 649 p. Disponible . [Consultado: Febrero 4, 2024].