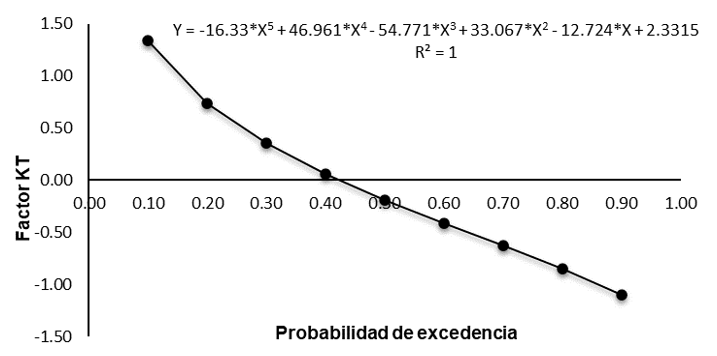
Estimación del factor de frecuencia Kt para la función de distribución de probabilidad gamma incompleta

Resumen

En este estudio se presenta un procedimiento para obtener el valor del factor de frecuencia de la Función de Distribución de Probabilidad Gamma Incompleta. a partir de los valores de los parámetros de forma (α) y escala (β). Mediante análisis de regresión se compararon las precipitaciones resultantes de aplicar el modelo de la variable reducida, con los obtenidos con la Función de Distribución de Probabilidad Gamma Incompleta. Se utilizaron datos de 53 años de precipitación total mensual de la estación meteorológica 27039 Samaria, Cunduacán, Tabasco; para ajustar y calibrar los valores del factor de frecuencia. Asimismo, se seleccionaron los valores de precipitación total mensual de cinco estaciones meteorológicas de varias regiones con agricultura de temporal de México, con registros que variaron de 31 a 59 años. Las estaciones meteorológicas de Motul de Felipe Carrillo Puerto, Yucatán; Texcoco, estado de México; Suchiate, Chiapas; Zapopan, Jalisco y Acaponeta, Nayarit, se utilizaron para validar los valores resultantes del factor de frecuencia. El coeficiente de correlación de Pearson en el proceso de ajuste, calibración y validación, fue superior a 0.997. Así, los valores resultantes del factor de frecuencia tuvieron muy buen ajuste y son confiables para calcular la probabilidad de excedencia de la precipitación total mensual para una Función de Distribución de Probabilidad Gamma Incompleta.